

Online writing service includes the research material as well, but these services are for assistance purposes only.
#SPECIAL RIGHT TRIANGLES DEFINITION HOW TO#
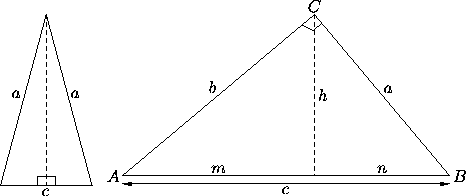
Then, you can learn how to find the third side of any triangle. Disclaimer: is the online writing service that offers 8 2 Homework Special Right Triangles custom written papers, including research papers, thesis papers, essays and others. There are more advanced trigonometric functions that allow us to calculate the third side of a triangle, even non-right triangles, given a particular degree angle and side length.īut either way, practice applying the Pythagorean Theorem until you feel confident with right triangles. There are two so-called Special Right Triangles that frequently appear. The Pythagorean Theorem helps us calculate the hypotenuse of a right triangle if we know the sides of the triangle. The other two angles are, by definition, complementary angles (x + y 90). If we substitute it into the formula, we get:Īnd by taking the square root on both sides, we figure out that the hypotenuse c = 5! Here we know the length of the side ( a = 3 and b = 4). But for now, let's see an example where we know the length of the sides and want to find the hypotenuse: Right Triangle Congruence Isosceles and equilateral triangles arent the only classifications of triangles with special characteristics. In fact, if we know the lengths for any two sides (leg A, leg B, and hypotenuse C) we can easily figure out the missing side by applying the formula. The Pythagorean Theorem states that for any right triangle, the sum of the squares of the lengths of the legs is always equal to the square of the length of the hypotenuse.īecause of the Pythagorean Theorem, it is easy to find the hypotenuse of a right triangle if we are given the sides of a right triangle. It related the length of the hypotenuse of a right triangle to the lengths of the legs (the legs of the triangle are the two shorter sides). The Pythagorean Theorem is a well-known theorem developed by a Greek mathematician named Pythagoras around 500 BC. The term 'right' triangle may mislead you to think 'left' or 'wrong' triangles exist they do not. In drawing right triangles, the interior 90 90 angle is indicated with a little square in the vertex. If a problem asks you to calculate the length of hypotenuse c in a triangle with side a, side b, and hypotenuse c, then you are working with a right-angled triangle. When one of those interior angles measures 90 90, it is a right angle and the triangle is a right triangle. It’s also the longest side of the triangle. "Hypotenuse" is simply a term that means "the longest side of a right triangle." The hypotenuse is the opposite side of the right angle in the triangle. Defining the Hypotenuseįirst, let's demystify this term. Let’s review this basic but foundational concept in trigonometry and how it relates to finding the hypotenuse of a right triangle. Plus, we can use it to find the base of a special right triangle and apply the converse of the Pythagorean Theorem. It makes the question of how to find the hypotenuse of a right triangle is easy to answer. The Pythagorean Theorem is an important theorem, as it comes up often in high school math.


 0 kommentar(er)
0 kommentar(er)
